世はまさに乱世であり、検査数が少ないのは政府の陰謀であるとか政府の無能であるとか政府はやっているとか、アメリカの陰謀だとかWHOは中国に操られているとか、無限に諸説ある中、グレートリセットが降臨すると言われている今日このごろですが、皆様いかがお過ごしでしょうか。
今日はこんな世情に背を向けて、ある病気に感染しているかどうかを見分ける検査がもっている確率論的な意味あいを考えていきます。確率論です。統計じゃなくて確率論。おじさん統計は全然解らないので。
疫病の検査においては、2種類のイベントが発生します。すなわち、
それぞれ\(I、 T\)とします。\(\sim I\) は感染してないというイベントで、 \(\sim T\) は陰性になる、というイベントです。検査では、患者が感染しているかどうかを知りたいわけですが、残念ながら100パーセント当たる検査というものは存在しない、というのは皆様なんとなく聞いたことがあると思います。詳しいひとならば「偽陽性」などという用語をご存知でしょう。つまり、
という場合があるわけです。上の例でいえば前者が偽陽性、つまり偽りの陽性です。
感染していれば必ず陽性になる検査を作るだけなら簡単で、当りのクジだけを用意しておけばいい。また逆に、感染してない人が陽性になることが絶対にないテストも簡単に作れて、それは全部陰性になるようなクジを作れば良いわけです。こういう極端で馬鹿げた例を考える事は案外無駄ではなく、ここから、カギは、イベント\(T\)がどれくらいイベント\(I\)を正確に再現できるか?という点にあることがわかってきます。
これは確率の世界では条件付き確率といわれているものです。条件付き確率は、あるイベントが起きたときに別のイベントが起きる確率です。 この場合でいえば、感染していたときに検査が陽性になる確率、あるいは検査で陽性になったときに実際に感染している確率です。理想的な検査は、 これが100%なわけです。
ところで、検査の性能として製品に伴って提供される情報としては、感染者をテストしたときにどれくらいが陽性になるか、あるいは感染してない人をテストしたときにどれくらい(まちがって)陽性となってしまうか、という情報です。これは条件付き確率で\(P(T/I)\)です。 しかしながら、我々が欲しいのはそうではなく、テストで+になったときに実際に感染している確率です。こっちは \(P(I/T)\) です。条件と本番が逆です。
$$ \frac{P(T\cap I)}{P(I)} = P(T/I) $$お馴染みの条件付き確率の定義です。この定義のうち何がどう「条件」なのか?という事を考えてみますと、 \(I\)の確率で割っているところは「その条件のもとで」ということで、ある意味自明ですから、実際に「条件と結末」にあたる構造が入っているのは「\(TかつI\)」の部分だという事がわかります。
それは、感染テストに引き戻って考えても当たり前で、つまり、感染していて検査結果が+になる、というイベントに対応します。たしかに ここがつかめれば疫病検査の確率論的な仕組みに一歩迫れるでしょう。
この式の両辺に\(P(I)\)をかければ\(TかつI\)の確率になりますが、それは\(P(I/T)\) についても同じです。まとめると
$$ P(I/T)*P(T) = P(T\cap I) = P(T/I)*P(I) $$こうなります。両辺を\(P(T)\)で割れば
$$ P(I/T)=\frac{P(T/I) P(I)}{P(T)} $$となって検査メーカー提供のスペックから我々が欲しい確率に一歩近づきます。あとは\(P(I)とP(T)\)がわかればいいわけです。
ところでこの式をじっくり見ると、
$$ P(I/T)=\frac{P(T/I)}{P(T)} P(I) $$とも読めます。\(P(I)\) は感染確率なので、それに \(\frac{P(T/I)}{P(T)}\) をかけたものが陽性になったときの感染確率というわけです。いま、この倍率を\(G\)とします。もし\(G\)が1よりも大きければ、このテストには意義がある、 といえるでしょう。なぜなら、\(P(I/T)\) のほうが \(P(I)\) よりも大きな値になるので、テストすることによって我々は疫病伝播の現状に一歩近づけるからです。 あるいはこの値が1ならば、ランダムに選んだひとが感染している確率と変わらないわけですから、テストはまったく無意味です。
これをもう一歩すすめれば、\(G\)の値でテストの意義を定量的に評価できるのでは?という発想につながります。1から外れているほど性能が良い、 あるいは、実施する意義がある、ということになるわけです。
意味の無いテストを考える事には、実は確率論的には案外、意味があります。もし\(G\)が1なら
$$ P(I/T)=P(I) $$です。これはつまり
$$ \frac{P(T\cap I)}{P(T)} = P(I) $$ということですから \( P(T\cap I) = P(I)P(T) \) となります。これはイベントIとTが独立だという定義ですね。たしかにそういうテストは無駄です。また\(G\)の値でテストを評価することには妥当性がありそうです。
テストはランダムに選ぶよりも確率をブーストしてくれる確率論的な装置と考える事もできます。
また、ここからただちに感染初期にはランダムに検査を行ってもほぼ無駄だという結論が得られます。すなわち、感染初期には\(P(I)\)は1よりもずっと小さい値になりますから、\(P(T)\)つまりランダムに選んだ個人の検査結果が+になる確率はほぼそのまま偽陽性の得られる確率です。つまり分母も分子も検査キットに付属する情報が そのまま使えますから、\(G\)はほぼ定数となります。また、その値もせいぜい一桁です。
そういう状況で検査を行ったとしても、得られた結果は元の確率と大して変わず、1よりもずっと小さい値のままです。
同様に、ほぼ全員が感染したゾンビ映画末期のような状況でも検査の意味が薄くなってしまいます。
疫病検査は、対象者が感染していると相当程度疑われる状況にないときに行っても意味が薄い、つまり、 検査の意義は、どうも\(G\)の値だけでなく、感染者の分布にも依存しているらしいという事がわかってきました。 ならば、どういう状況にあるときに行えば、検査には意味があるのか? あるいは、相当程度疑われる状況って何だ?という疑問がうかびあがってきます。
ほとんどが感染してない(あるいはしてる)状況ではテストに意味が無いのなら、 その逆の、感染が半々だったら意味がありそうです。
そこでイベント\(X\)について下の式で定義される量\(H\)を導入します
$$ H(X)=P(X)\log \frac{1}{P(X)} +P(\sim X)\log \frac{1}{P(\sim X)} $$上式は「情報エントロピー」と言われている量です。 2値のイベントならば、その確率が半々の時にエントロピーは最大になります。 感染してるかどうかの確率が半々、つまり、一番事情が不確かなときに値が大きくなるという事は、 それだけフタを開けてみる価値が高い、という事です。
結合イベントI & TについてもHを定義でき、その場合は \(I, T \)それぞれが成り立つ場合、成り立たない場合合計4つの場合について列挙して合算した ものになります。この値がいくつになるかは \(I, T \)の間にある関係に依存しますが、もし無関係(つまり独立)だった場合は\(P(X \cap Y) = P(X) P(Y)\) であることから \(H(X\cap Y)=H(X)+H(Y)\) となります。
同様に条件付き確率についても情報エントロピーを考える事ができ、それは
$$ H(X/Y)=H(X\cap Y)-H(Y) $$となります。
\(H(I)とH(I/T)\)を比べたら、\(H(I/T)\)のほうが少なくなります。テストをやったことで感染に関する情報が得られるからです。 もっとも、かならずそうなるとは限らないという事は先の独立性に関する考察からわかります。
条件付き情報エントロピーの定義から、
$$ H(I/T)+H(T)=H(I\cap T)=H(T/I)+H(I) $$が成り立ちます。
ここから、以下のようにして先の\(G\)という倍率の対応物は情報エントロピーにも\(H(T)-H(T/I)\)として存在し、しかもそれは 素の感染事象が持っているエントロピー\(H(I)\)と、検査で陽性になったという条件つきエントロピー\(H(I/T)\)の差と等しいことがわかります。
$$ H(I)-H(I/T) = H(I) - (H(T\cap I) - H(T)) $$ $$ = H(I) + H(T) - H(I, T) $$ $$ = H(T) - (H(I\cap T) - H(I)) $$ $$ = H(T) - H(T/I) $$そして検査で稼げるエントロピーは、個別のエントロピーの和\(H(I)+H(T)\)と、結合エントロピー\(H(I\cap T)\)の間の差に対応していた事がわかります。
それでは、テストの性能と感染者の分布によって、テストで得られる情報エントロピーがどう変わるかを実際に調べてみましょう。下はテストの性能に関する2とおりのパラメタについて、テストで獲得されるエントロピーが感染者の分布でどう変化するかをプロットしたものです。 左は適合率、再現率ともに99%の場合、右は70%の場合です。
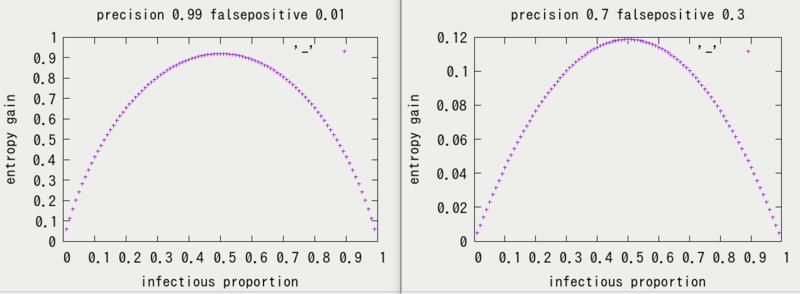
いずれの場合も、感染者が半々の場合がもっとも情報の利得が大きくなり、感染者が非常に少ない場合は利得がほとんど無くなる事がわかります。 これはもともとの感染現象が、蓋をあけてみるまでもなくわかりきっているため、検査をやる意味が無い、という状況ともよく一致しています。
また、下のプロットからは、感染者が少ない場合には精度(適合率)よりも再現率(間違って+を出さない性能)の改善が有効である事がわかります。 多数の健康な人が誤判定で紛れ込んでくることが情報利得の妨げになっており、これを遮断できれば検査で獲得できる情報が増大するわけです。
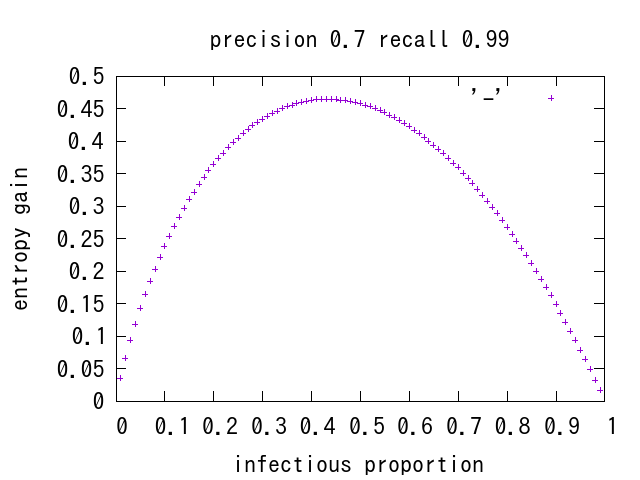
ピークも左に若干シフトして4割程度の感染者の場合に検査が最大のパフォーマンスを発揮することがわかります。
演習 精度50%のテストは意味があるか無いか。あるとすればどういう性能が必要か。
演習 雑に「こうなります」などといって適当に自然言語でごまかしたステップを証明で繋いでください。