プログラムで生成される乱数は大抵一様分布なわけですが、 そこからチョイとひねってやればいろんな分布の確率変数を生成できるのでは ないか、というのは誰しも思い付くところではないでしょうか。
とりあえず中心極限定理を使えば正規分布は作れます。 足して割ればよい。
def clgauss(mean=0, var=1.0)
sigma=Math::sqrt(var)
sigma*(Array.new(12){rand(0)}.inject(0){|r, v|r+=v}-6.0) + mean
end
極限定理とかいってるわりに12個しか足してませんが。
もちっと洗練されたやりかたとしては、 Box-Muller transformation \(\sqrt{-2\ \ln x_1} \cos(2\ \pi\ x_2)\) を使う方法があります。
Math::sqrt(Math::log(rand(0))*(-2))*Math::cos(2*Math::PI*rand(0))
Ruby で普通に計算している分には、さすがにこちらのほうがだいぶ高速ですが、 このあたりは処理系の実装に依存するところが大きいと思います。
正規分布が作れれば、これの派生は大概作れますね。
目標とする分布の累積分布関数の逆関数の引数に一様分布変数をとれば、 その分布の確率変数が得られます。 これに気づいた俺すげぇと思いましたが、 朝になって、こんなの誰も知らないわけねぇと思って調べてみたら、 ちゃんと名前がついていました。 逆関数法 inversion method とか inverse transform sampling というそうです。 証明ですが、分布関数 \(D\) の逆関数 \(D^{-1}\) が一様分布な確率変数を 定義域としたとき、その確率空間は \(D\) と同じ分布関数を持つという事をチェックするわけで 定義からほぼ自明です。
そのままアルゴリズムとして使えます。 関数をファーストクラスオブジェクトとして持つような 処理系ならば、数行で実装できます。
def rand_cdfinvert(&cdf) cdf.call(rand(0)) end
Ruby での実装はこれにて終了です。 それでは手始めに巾が4の巾分布を作ってみましょう。 巾分布の累積分布関数の逆関数 $$\frac{b}{(1-x)^{1/a}}$$ を rand_cdfinvert にブロックで渡します
irb(main):252:0> rand_cdfinvert{|x|3/(1-x)**0.25}
ブロック変数に一様分布の確率変数 rand(0) が 入って、巾分布な確率変数のできあがりです。 うえは巾が4の場合です。
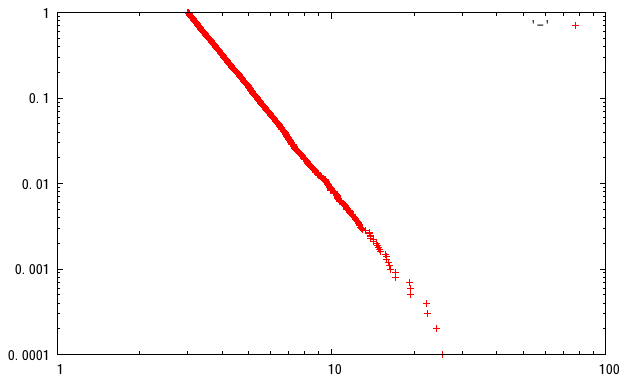
ウホ。良い巾分布。では、できあがった確率変数の巾を検算代わりに最尤推定してみましょう。
irb(main):265:0> Array.new(10000){rand_cdfinvert{|u|3/(1-u)**0.25}}.sort.mle_power
3.9616135523218
mle_power は巾分布の巾の最尤推定です。 だいたい合ってますね。 inverse transform sampling は、累積分布関数の逆関数が簡単に計算できるものには、 数学的な内容が自明と言えるほど直観的で、非常に使いやすく解りやすい方式だと思います。
今回は MathJax というのを 使って \(\TeX\) で Web に数式を書いてみました。 \(\TeX\) を書くのは何年ぶりでしょうか。 MathJax は、簡単にインストールして使えるので、 \(\TeX\) を使った事があれば憶える事もやる事も少なくて良いと思います。
他にも様々な分布に応じた確率変数の生成手法があるようですが、 とりあえずこの項はこれにて。