たまにこういう問題みかけます

こんなんいちいち人間が解くのは俺は癪に障るのだ. ということで, 計算機に解かしてみましょう. ってどうすんの?
考えててもしょうがないから, とりあえずぱっと見てみますか. ぱっとグラフで.
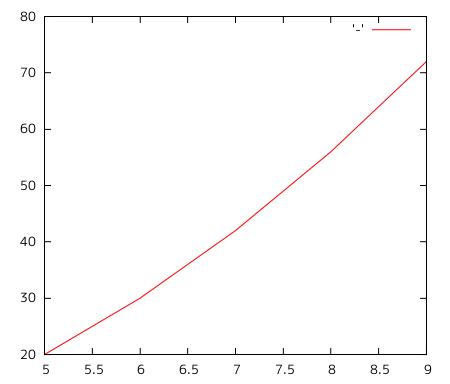
ぱっとみ明らかに2次曲線ですやんこれ. ということは, 一般的にいって $$ax^2+bx+c$$
なわけですよ. あとはこれに合うような \(a b c\) を計算したらいい. でもどうやって?
そりゃズレてる量を計算する関数でも作って, その値が一番小さくなるような \(a b c\) をなんか最適化を使って求めたらいいんじゃないの? ズレは, データの点5つ分について, それぞれ \(ax^2+bx+c\) の値と72, 56, 42, 30, 20 の差の二乗を計算して, それを合計する, 二乗誤差と世間で言われているやつでやってみよう. ということで, まずは与えられたデータを入力
irb(main):210:0> vals=[[9, 8, 7, 6,5], [72, 56, 42, 30, 20]] [[9, 8, 7, 6, 5], [72, 56, 42, 30, 20]]
次は, 二乗誤差を計算する関数をつくろう.
定数 \(a, b, c\) と入力データ \(x, y\) を使って, $$(ax^2+bx+c - y)^2$$ の和を計算する関数を無名関数として作る
irb(main):211:0> evl=lambda{|a, b,c|vals.transpose.map{|x, y|(a*x**2+b*x+c - y)**2}.sum}
次は, これを最小とするような定数 \(a, b, c\) の組を多次元最適化を使って計算.
irb(main):212:0> evl.dhsmplx([[0, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 1]]).last [[0.9999999999999998, -0.9999999999999982, -3.138320561930072e-15], [1.0, -1.0000000000000018, 1.1483498887881563e-14], [1.0, -1.0000000000000009, 6.6434310532595005e-15], [1.0, -1.0000000000000002, 4.996203126403663e-15]]
つまり \(a=1, b=-1, c=0\) ということらしいので, この関数は $$x(x-1)$$ だったというわけです.
ホンマに合ってる? おー, 合ってるわ. すげぇ(自画自賛)
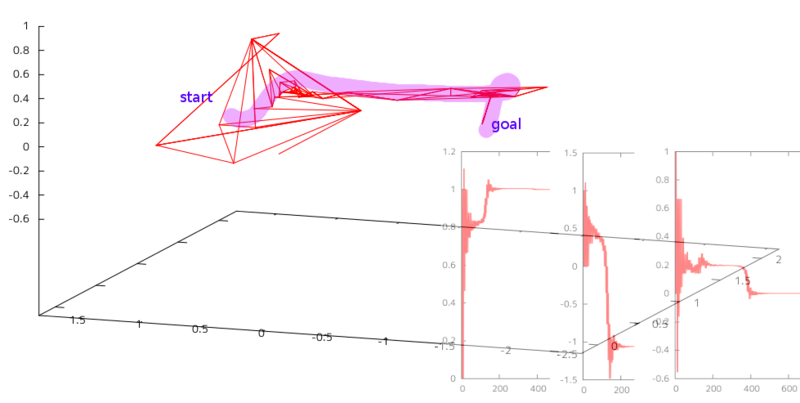
収束の過程を3次元グラフ化してみました.右下の半透明3つはx軸, y軸, z軸それぞれの動きです. xもyも200ステップぐらいで正解に収束しているが, zが400ステップぐらいでやっと正解に収束している.
よく西部劇とかで風に転がる草があるけど, あれって英語で何ていうんやろね? と思ってしらべてみたんよ. そのものずばり「風で転がる草」で検索したらすぐ分かったわ. tumbleweed っていうねんな. そんままやん.
tumbleweed で検索すると, 平原を埋め尽くしてころがっていく tumbleweed の動画がものすげぇたくさんヒットして, どうもアメリカの一部地域では tumbleweed (もうめんどくさいので以下tとだけ書きます) の撮影が重要な娯楽になっているらしいことがわかる. なってない. 非常に深刻な問題なのであるらしい. なんせうちの出入り口が積み上がった t で埋まってしまって出入りできないとか, そういうことになってる.
そこで, t を効率的に片付ける方法はないものか, と t がいっぱい生えているところで研究が行われているらしい.
ところで t のサイズってどういう分布なんだろ? やっぱし正規分布かね? 日々の成長の積み重ねということで.
tは, 成長したら根元のところでぽっきり折れて, 転がってるときに種が地面におちて, 増える. そういう戦略で分布を拡大するんだって. 漢字では「転蓬」と書くらしい.